There are many ways to get analogue outputs from the Arduino Uno (ATmega328P), which is otherwise limited by it's lack of an inbuilt DAC. 'Embedded newbie' did a good job of describing the different techniques in use.
Embedded newbie's blog - Review of Arduino DAC solutions (2011)
Generally the solutions can be categorised as the following:
- Dynamic methods: Pulse Width Modulation (PWM), and capacitor integrators.
- Static methods: Resistor ladders and networks.
- Attaching a DAC IC via parallel or serial connection.
Most of the static designs use an R-2R resistor ladder (which is described on
wiki). When a resistor ladder is used each binary code translates to a voltage level, offering 2^n output levels using n-pins of the Arduino. The exception is the cheap '2-cent' DAC which only scales linearly.
But there is always room for the esoteric and eccentric, and it's possible to build static DACs which produce more output levels per pin used. It's possible to make a 16-level (4-bit) static DAC driven from just 2-output pins (Skip to the result:
16-level DAC using 2-pins). While 16 levels might not sound like much, not all applications require high fidelity, think analogue control instead of audio reproduction!
Static DAC Designs
The '2-cent' DAC
This DAC uses a single external resistor to produce a range of output voltages. It's not very efficient as a DAC because it only scales linearly, producing (n+1) output levels for n I/O pins.
The output voltage can be calculated:

In the original description (2011) the suggested value for the external resistor was equal to the internal pull-up, but this produces a non-linear response (unless that is what you are after). Using a smaller external resistor value results in a more linear spacing of levels. This is at the lowest effort end of DACs!
2-cent DAC description
R-2R resistor ladder designs
The I/O pins from the device are connected to Vb0..3 with Vb0 representing the least significant-bit. The output is available at Vo3. The simplest way to consider the R-2R DAC is that each stage is a voltage divider of the previous stage with the ratio set to 1/2.
Considering only stage 0 (as if stages 1-3 were disconnected)
The Thevenin equivalent circuit for the first stage also has a resistance of 1R (2R||2R), so in stage 1 a further 1R is added in series to make 2R in both branches.
Ignoring the later stages (as if disconnected) and using Vo0 calculated previously
And this repeats for the final stages
This correctly weights the pins to produce an analogue approximation of a digital signal, and given that the DAC can be constructed with a single resistor value (with 2 in series or parallel to achieve the R-2R ratio) explains it's popularity.
Resistor ladder wiki.
R-2R DAC practical design.
Trinary/Ternary DACs
But it's possible to do better than this, a microprocessor pin actually has at least three states. When set as an input the pin is high impedance (effectively disconnected except for a small capacitive load). On it's own this isn't particularly useful, as the ladder-type DACs require voltage outputs, but it can be adapted using a carefully sized voltage divider. The idea was documented by 'Raronoff' in 2011.
Raronoff - Trinary/ternary ladder DAC
The adaption is biasing the pins so that when the output is in the high impedance state the voltage is held at Vs/2. The model for the pin is roughly (ignoring the drive resistance)
If the resistance Rb is large enough that it can be easily overpowered by the chip output then the equivalent model for a pin becomes as follows.
Rb must be chosen to prevent excessive current from the output when driving '1' or '0'. Raronoff suggests the absolute minimum size for Rb=120, however this causes around 40mA of current to flow through the pin, which is the absolute maximum rating. By this point the pin voltage could droop up to 1V according to the datasheet, and isn't likely to be a stable operating point. Instead a resistance of 1k and upwards will limit the output Voltage drop on the pin to a point in the linear region.
Now that the pin output looks like a three state voltage source, it can be used to construct a DAC, as described in a paper from 1979, and linked by Raronoff. This DAC can produce 3^n outputs where n is the number of input 'trits', in this case the I/O pins.
Ternary to Analog converters using resistor ladders (1979).
The biased pin is still far from an ideal voltage source, as the voltage levels have a different series resistances. The solution is to hide this as much as possible by making the resistors used in the DAC large in comparison to the bias resistors Rb.
A trinary DAC will then look something like this, I have biased the first stage to Vs/2 instead of 0.
Each stage of the DAC the should now contribute 1/3 to the next result instead of 1/2, and so the resistance ratios must be adjusted. Given a choice of Ra (which is at least an order of magnitude larger than Rb) the divider must have a ratio of 2:1.
The output can then be calculated
Here are some resistor values which provide a near linear output for a few 'trits' based on spice simulations. The 4/3 ratio isn't present in E12 resistors, but is available with E24, 75k:100k.
Ra = 75k
Rc0 = 150k
Rc = 100k
Rb = 2.2k
Rs = 25 (AVR datasheet typical)
There is an unavoidable glitch when using 'trinary' DACs on the AVR, as discovered in the original blog. For a standard R-2R DAC all of the pins can be switched with a single OUT instruction by using pins from the same PORTx register. On the AVR it is not possible to change the direction and drive-value of pins with a single instruction, resulting in a glitch output between the updates. The duration of the glitch can be minimised by ensuring that the update code uses two OUT instructions consecutively, limiting the duration to one clock period, about 63ns. Ideal solutions for removing the glitch such as a sample-and-hold circuit on the output of the DAC are overkill for a 'cheap' solution.
An example using 3-state control:
A 9-bit microcontroller-driven DAC.
Quaternary/ 4-ary DAC
If I said there was more, you might guess where I was going. The Arduino I/O pins actually have 4 possible output configurations. If a '1' is written to the PORTx register when the pin is configured as an input then the internal pull-up resistor is activated. This resistor isn't exactly a precision component and will vary between chips, but it does increase the possible configurations of the pin, allowing 4^n outputs. (As I found in the
previous blog post it's not even a true resistor.)
To accommodate this there is a slight change to the biasing circuit:
With the equivalent model:
In order to use this output to drive a resistor-ladder DAC the voltage levels Vs0..3 must be evenly spaced. The range of effective voltages Vs0-Vs3 might be less than the supply voltage, the full range only occurs when there is no external pin resistor (Rp=0).
By first calculating the effective voltages Vs0..3 the equations can be solved by setting Vs1 equal to 1/3 of the Vs0-Vs3 range, and Vs2 = 2/3 of the range.
The equations have a free variable, either Rp or Rb2 can be chosen. The simplest case is setting the resistor Rp=0. A non-zero Rp reduces the output range for the pin, but also has the benefit of decreasing the effective output resistance as the corresponding Rb2 will be smaller. (This ends up being significant later on, as the DAC has a high output resistance)
Which for the values measured
previously (Rpu=34.4k, Vpu=4.77V) gives
Rb2 = ~60k (59.7k)
Rb1 = ~120k (119.5k)
With these values I get the following voltages
'0' -> 0.005V - 0.010V
'1' -> 1.632V - 1.633V (Ideal 1.667V, error=0.7% FSR)
'2' -> 3.34V - 3.35V (Ideal 3.333V, error=0.3% FSR)
'3' -> 5.01V - 5.015V
Clearly my measurements weren't perfect, but the internal pull-up resistor isn't exactly a precision component! It's likely to vary with temperature and voltage anyway, and will be slightly different between each pin.
With Rp=0 this is far from an ideal voltage source, the series resistance varies between 25R and 40k depending on the voltage level. The ideal solution at this stage would be to buffer the resulting voltage level with an op-amp, but this doesn't really fit the Lo-Fi nature of the design. Instead the only option is to make the connected load resistor sufficiently large that the range (0-40k) appears constant, but if the resistor is too large it will have trouble driving even a small capacitive load.
The values gained by setting Rp=0 are not necessarily the most practical values. One side effect of the equations is that when driving a logic '2' using the internal pull-up resistor the voltage at the chip pin will always be 2/3 of the supply irrespective of the chosen Rp and Rb2. This simplifies characterising the value of the internal resistor to a single point on the I/V curve.
Making a DAC
Now at each stage the voltage divider should reduce the input from the previous stage to 1/4 of the full scale range. This requires an effective resistance ratio of 3:1 between the previous stage and the pin resistor.
The resistor ratio 9/4 (2.25) doesn't occur exactly, but a ratio of 2.2 is easy to achieve, and for a reason I will get to later it is better to have a ratio slightly below the target.
To construct a 2-pin DAC I used the following values:
Rc0 = 1M (2M divider from Vs to Ground)
Ra = 330k (8x the Rb2||Rb1 impedance)
Rc = 736k (680k+56k, target value 742k)
Rb1 = 119k (alternatively use 120k)
Rb2 = 60.7k (56k + 4.7k)
The DAC is driven from digital pins 2&3 on the Arduino Uno header. It's not possible to use digital pins 0&1 because these have other connections on the board.
The output was measured by connecting it directly to an ADC input. This is not ideal because the effective output resistance of approximately 220k is too high to drive the ADC! A plot of the voltage readings used to produce the result shows a low frequency drift of about 1% FSR in addition to the noise.
The output levels look reasonably linear, as confirmed by the Integral Non-Linearity (INL):
The measured INL is about 0.22 LSB, which is 'good enough' to call this a 4-bit DAC.
AC Performance.
16ms ramp (31Hz triangle)
0.4ms ramp (1.2kHz triangle)
40us ramp (12kHz triangle)
The AC performance is limited to around 10kHz, possibly due to the large resistor values used in the DAC, and the effects of load and stray capacitances. For any practical purpose the DAC requires an output buffer - even connecting a cheap £5 multimeter has a significant impact on the DAC output voltage! Ideally an op-amp voltage follower on a higher supply voltage, or a voltage divider on the output.
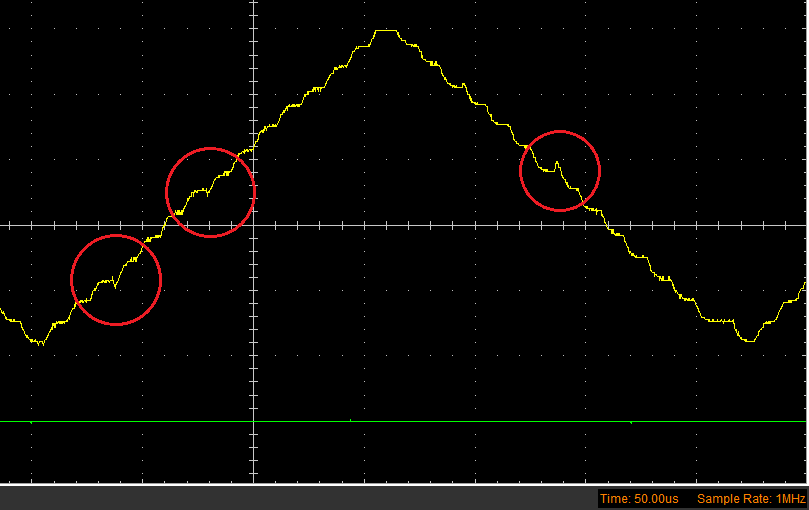
Several glitches are visible in the transitions for the 1.2kHz triangle wave. Initially I believed these might have been due to the 63ns delay between the two instructions which update the pins (which have to be used explicitly to avoid compiler rearrangements).
__asm__( "OUT PORTD, %0 \n\t"
"OUT DDRD, %1 \n\t"
:
: "r" (value), "r" (direction)
:
);
However increasing the delay between the two instructions doesn't lead to a corresponding increase in the glitch. The pins on the chip itself have very fast rise and fall times (on the order of 10ns), but it is possible that one of the high impedance transitions such as enabling the pull-up resistor is significantly slower in overcoming the parasitic capacitance.
Updated: the largest spikes occur with the trasnsition of the MSB from driven to high impedance, these glitches can be reduced, see:
Reducing the ladder-DAC glitches.
Extending the DAC precision.
Why stop at 2-output pins (4-bit equivalent) DAC? The answer is that these components are all poorly matched, and further bits will start to yield diminishing returns. As the number of bits increases the range will become discontinuous, with overlaps and gaps which occur when one of the MSBs transition.
There is a solution to this resolution limit, which can hide static mismatches, but not drift due to temperature. This is to design the DAC with more output levels than are required, and to calibrate and store the required codes in a lookup table. This works providing there is guaranteed to be an output voltage level within a certain range. To achieve this the potential divider equations must be revisited to guaratee that there are no gaps in the output range, which can be done by overlapping the voltage levels from the previous stage.
An example 4-state control DAC:
An 8-bit static DAC using only 4 I/O pins.
It's also probably a good idea to abandon the internal pull-up resistor, the 4-ary DAC might be a novelty!